Charge relaxation in a reservoir filled with electrified liquid

Stefan Stefanov1, Ivan Prodanov2

 

1 University of Mining and Geology “St. Ivan Rilski”, 1700 Sofia,

2 University of Mining and Geology “St. Ivan Rilski”, 1700 Sofia, e-mail: enemko@mail.bg

 

ABSTRACT. This study observes the process of charge relaxation in a reservoir filled with electrified liquid, containing positively and negatively charged particles with volume density, as a function of the state of the liquid inside the reservoir, and of time.

 

Key words: static electricity, charge relaxation

 

РЕЛАКСАЦИЯ НА ЗАРЯД В РЕЗЕРВОАР, ЗАПЪЛНЕН С НАЕЛЕКТРИЗИРАНА ТЕЧНОСТ

 

Стефан Стефанов1, Иван Проданов2

 

1 Минно-геоложки университет “Св. Иван Рилски”, 1700 София,

2 Минно-геоложки университет “Св. Иван Рилски”, 1700 София, E–mail: enemko@mail.bg

 

Резюме. Разглежда се процеса на релаксация на заряд в резервоар, запълнен с наелектризирана течност, съдържаща положително и отрицателно заредени частици с обемна плътност, явяваща се функция на положението на течността в резервоара и на времето.

 

Ключови думи: статично електричество, релаксация на заряд

 

Introduction

 

   Contemporary multi–tonnage production requires high efficiency of the pipeline transport; therefore, limiting transportation speed to the safe values of between 0.7 and 1.4 presupposes the use of costly wide-diameter pipes.

 

   Loading the apparata and tanks through a vertical pipe that has been lowered almost to the bottom ensures the safe liquid feed at a considerably high rate (permissible outflow rate). First, however, this type of feed is not always possible to ensure, and second, the permissible feed rates for liquids with high density charges are not that high. In both cases, it is necessary to use special gadgets that reduce electrification of the liquid flow along the pipeline and create more favourable conditions for discharging of the charge resulting from the free jet which moves below the liquid layer and the surface liquid in the tank.

 

Relaxation vessels of various structures are the most common means of reducing the value of the charge that is transferred to the tank from the jet outgoing from the pipeline [1].  The relaxation vessel of a relatively small size is placed on the feed pipe at the very inlet of the tank or apparatus. While residing in the relaxation vessel, the liquid gives off to the walls a larger part of the charge that has been transferred by the pipeline, exits the pipeline, and moves to the major tank or apparatus already relatively weakly charged. To avoid a possible inside blast, the relaxation vessel must all be filled up with liquid. The relaxation vessel must have such volume which ensures that the liquid residence time in it considerably exceed the relaxation period of the charge.

 

 

   This report examines the process of charge relaxation in a reservoir filled with electrified liquid containing positively and negatively charged particles with volume density as a function of the position of the liquid in the tank, and of time.

 

Exposition

 

    A random shape volume with a surface area equal to is studied. The volume is filled with electrified liquid containing positively and negatively charged particles with volume density and , that are the function of the position of the liquid in the reservoir, and of time. The liquid charge is

 

.    (1)

 

   The charge current in is equal to

 

,   (2)

 

where is the current density through surface, .

 

   Employing the vector equation

 

,    (3)

 

We can put down

 

.  (4)

 

   As far as the discussed volume is random, integration can be omitted

 

.   (5)

 

   Let’s establish the relation between current and intensity of the electrical field that generates the liquid charge

 

,    (6)

 

where is the ion mobility factor in the liquid, , and , , is the vector of the intensity for the electrical field that generates the liquid charge.

 

   In conformity with Poisson’s equation 

 

,   (7)

 

where is the absolute dielectric permeability of the void: and   is the relative dielectric permeability of the liquid.

 

   Combining equations (5) and (6) we get

 

 (8)

 

   Equation (8) is the output for determining the law of liquid charge relaxation.

 

   It is generally considered [2, 3] that with liquids with specific electrical resistance of and less the degree of electrification does not influence electrical conductivity, i.e. under various conditions and with different liquids we have a sufficient amount of charge carriers from the two polarities, in other words

 

   In this case

 

   (9)

 

where is the electrical conductivity of the liquid, .

 

   Upon substitution of equation (7) in equation (8), and taking into account equation (9), we obtain the differential equation

 

,   (10)

 

where is the time-constant of the liquid relaxation, .

 

   The solution to equation (10) is of the type

 

,   (11)

 

   Multiplying equation (11) by volume, we get the total liquid charge

 

,    (12)

 

Where and are respectively the total liquid charge, , in the beginning and  at a random point of time.

 

   Equation (12) is the law of liquid relaxation.

 

   As long as , the charge relaxation rate is entirely determined by its specific electrical resistance , , since does not actually change in dielectric liquids  with the change of electrical conductivity.

 

   In conformity with equation (12), charge relaxation is commonly called Ohm’s relaxation or Ohm’s law.

 

   For liquids with a rather high specific electrical resistance (), where the number of charge carriers determining their electrical conductivity is small, it would be incorrect to assume that  the complete number of carriers during the process of liquid excitation is constant. In this case it is assumed that the charging liquid contains carriers of only one polarity since the charges of one polarity are removed during excitation and charges of the opposite polarity are added. As a rule, electrical conductivity of such a liquid may exceed the initial conductivity due to excitation. Bearing in mind the above assumption, and considering the charge distribution as uniform throughout the whole volume, equation (8) is transformed into

 

,    (13)

 

   In this case, is the charge density with one plus or minus sign, depending on what the sign of the electrifying liquid is.

 

   The solution to equation (13) is

 

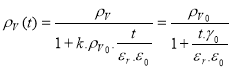, (14)

 

where is the electrical conductivity of the electrified liquid and is the charge density of the liquid at point .

 

   Multiplying the left– and the right–hand sides of equation (14) by the volume of the liquid, we obtain Ohm’s law of the relaxation of the liquid volume charge

 

,   (15)

 

Conclusion

 

   As follows from equation (15), the value of the charge decreases in time according to a law that is similar to the hyperbolic law. In relation to this theory, the relaxation of a liquid whose electrical conductivity is less than   is generally referred to as hyperbolic.

 

   According to equation (14), relaxation depends only on the initial charge density and on the ion mobility.

 

  In the intermediate range of liquid electrical conductivity, , the process of charge relaxation is described as a combination of Ohm’s law and the hyperbolic theory. In this case, the conductivity of the uncharged liquid is reported.

 

Литература

 

[1] Стефанов, С., И. Проданов. Статично електричество – теория и практика. С., Авангард Прима, 2013. (Stefanov, S., I. Prodanov. Statichno elektrichestvo – teoria i praktika. Sofia, Avangard Prima, 2013).

[2] Захарченко, В. В, Н. И. Крячко, Е. Ф. Мажара, В. В. Севриков, Н. Д. Гавриленко. Электризация жидкостей и ее предотвращение. М., Химия, 1975.

[3] Бобровский, С. А, Е. И. Яковлев. Защита от статического электричество в нефтяной промьшлености. М., Недра, 1983.