Аналитичен метод за изчисляване несиметрията на напреженията в трифазните електрически системи
Стефан Стефанов 1, Иван Проданов 2
1 Минно-геоложки университет “Св. Иван Рилски”, 1700 София,
2 Минно-геоложки университет “Св. Иван Рилски”, 1700 София
Резюме. В доклада се третира проблем, разгледан в литературата към него, като се предлага друг аналитичен подход за определяне на формулата за несиметрията на напрежението. Полученият краен резултат е по-удобен за практическо ползване. Изведен е израз за определяне фазата на вектора на напрежението с обратна последователност.
ANALYTICAL METHODOLOGY FOR CALCULATING ASSYMETRY OF CURRENTS IN THREE-PHASE ELECTRICAL SYSTEMS
Stefan Stefanov 1, Ivan Prodanov 2
1 University of Mining and Geology “St. Ivan Rilski”, 1700 Sofia,
2 University of Mining and Geology “St. Ivan Rilski”, 1700 Sofia
ABSTRACT. In this report, a problem is examined throughout the literature, where another analytical approach for determining the formula of asymmetry of currents is being proposed. The final result is more convenient for practical use. An equation is derived for determining the phase of the voltage vector with reverse order.
Въведение
Прието е несиметрията да се характеризира със стойностите на напреженията и токовете с обратна и нулева последователност на основната честота. Появата на тези съставки се обуславя от наличието на несиметрично натоварване и аварийни режими в електрическите трифазни мрежи.
Несиметрията на напреженията на изводите на консуматорите на електрическа енергия количествено е регламентирана в [1].
Появата на съставки с обратна и нулева последователност на напрежението (
и 
) и на тока (
и 
) довежда до увеличаване на сумарните токове в отделните фази на мрежата, вследствие на което по условието на нагряване се намалява допустимия за тях ток с права последователност. Появата на напрежение с обратна последователност на изводите на въртящите се електрически машини е причина в роторните им намотки да се индуктират е.д.н. и токове с удвоена честота. Те предизвикват допълнително нагряване на машините.
Появата на напрежения и токове с обратна и нулева последователност оказват вредно въздействие върху нискочестотните канали на съобщителните връзки и уредбите за сигнализация, влошавайки тяхната нормална работа.
В доклада се третира проблем, разгледан в [2]. Предлага се друг аналитичен подход за определяне на формулата за несиметрията на напрежението. Полученият краен резултата е по-удобен за практическо използване. Изведен е израз за определяне фазата на вектора на напрежението с обратна последователност, липсващ в [2].
В някои случаи определят несиметрията на напрежението, като отношение на напрежението с обратна последователност, към номиналното напрежение:
[%] (1)
Такава оценка на несиметрията, при вероятностен характер на консумацията на енергия в големи количества от съвременни технологични консуматори, довежда до значителна грешка. При това грешката е толкова по-голяма, колкото е еднозначното отклонение.
Възприето е несиметрията да се оценява като отношение на напрежението с обратна и права последователност [1]:
[%] (2)
Това се обяснява по следния начин. При големи еднофазни отклонения напрежението 
губи своята номинална стойност и се превръща в число, което не е свързано с режима на несиметрията. Затова изчислението по формула (1) довежда до грешка, която расте с увеличаване на еднозначното отклонение.
Аналитичен подход за определяне на формулата за несиметрията на напрежението
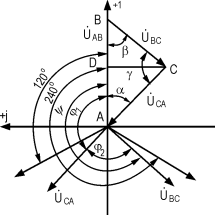
Разглеждаме векторната диаграма на междуфазовите напрежения на трифазна система в несиметричен режим, показана на фиг.1.
Фиг. 1.
Независимо от схемата на съединение на намотките на захранващия източник и на консуматорите на електрическа енергия, геометричната сума на линейните напрежения е равна на нула (като сума на напрежението по дължината на затворен контур, съединяващ изводите на фазите А, В и С):
(3)
В съответствие с векторната диаграма напреженията с обратна и права последователност имат вида:
(4)
(5)
където 
е фазовия оператор; 
; 
, 
– ъглите между векторите на напреженията 
и 
, 
и 
; 
и 
– фазовите ъгли на напреженията с права и обратна последователност.
От векторната диаграма следва: 
и 
.
Ъглите 
и 
се намират, използвайки косинусовата теорема:
;
.
Изчисляването на несиметрията може да се опрости. Спускаме перпендикуляр от върха С на триъгълника АВС към страната АВ, записваме:
; 
; 
,
където 
; 
.
Замествайки стойностите на векторите в изрази (4) и (5), след преобразуване получаваме:
(6)
Модулите на напреженията с обратна и права последователност се определят с изразите:
(7)
(8)
От векторната диаграма следва:
,
където 
.
Величината 
(лицето на триъгълника АВС) се изчислява по формулата (3):
,
където 
.
От съотношението на страните на триъгълниците АВС и ВСD имаме:
(9)
а
(10)
След заместване на (10) в (9), при 
, получаваме:
.
Фазата на вектора на напрежението с обратна последователност се определя от изразите:
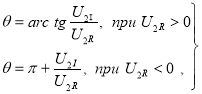(11)
където 
и 
са действителната и имагинерната съставки на напрежението с обратна последователност.
Стойностите на 
и 
се определят с формулите:
(12)
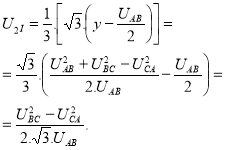(13)
Изводи
1.Предложен е аналитичен метод за точно изчисляване несиметрията на напреженията с измерване и използване на техните модули.
2.Изведена е формула за фазата на вектора на напрежението с обратна последователност.
3.Предложената методика позволява да се анализира несиметрията на режима на системите на електроснабдяване на промишлените предприятия с цел определяне пътя на тяхната оптимизация.
Литература
[1] БДС 10694 – 80. Норми за показателите на качеството на електрическата енергия при приемниците.
[2] Стефанов, С. 1996. Критерии за оценка на несиметрията на напреженията и токовете в трифазни електрически системи. Год. МГУ “Св.Ив.Рилски”, т. 41, св. IV.
[3] Бронштейн, И. Н., К. А. Семендеев. 1986. Справочник по математике для инженеров и учащихся вузов. М., Наука.
